Introduction⌗

In this post I plan to give an introduction to reversible programming languages, and some introduction to the programming language Rust. Then I will introduce my amalgamation of those two things, RRust. The overview I will give here is not going to be too deep, In the end, I will provide some articles which go deeper into it all. RRust was produced for my Master’s Thesis, so the recounting here goes into some details which may already be known to Rust users. Finally, any comments or questions are welcome and can be sent to blog@erk.dev.

Reversible Computing⌗

Introduction⌗

Reversible computing is the idea that you can for a given function f(x) := y you can generate the inverse function that takes the output and generates the input f^-1(y) := x. This of course could be done by hand, but we want to make a machine, here donoted by I, that can make the transformation of the code. That is that I(f) := f^-1. To generalize this a bit we can look at x and y as states and f as a function that goes from state x to state y, this is how we will look at it in the following chapters since we are going to model our functions as mutations to variables. So we want to generate the inverse function f^-1 that takes state y and mutates it to state x.

Which Functions Can Be Reversible?⌗

A good question to ask here is if all functions can be reversible or if there are some limitations here.

So the first thing we can single out here is that we need the functions to be deterministic, that is that for any given input the function will always produce the same output, but we have to go a bit further than that here. We also need backward determinism, that is that any output can only be produced from a single input, which can also be seen as that the inverse function is deterministic.

From this, we can see that a given function will have to be bijective.

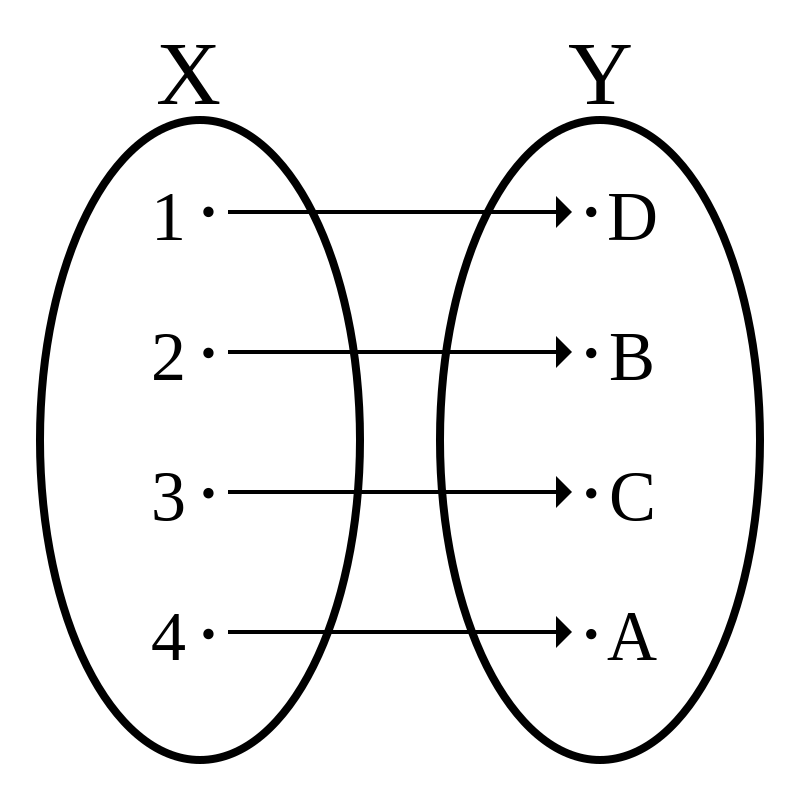
There is a small caveat to this, we cannot always know before a computation if it will succeed, so we need to include a third possibility, in the form of an error. So any function is reversible if it is bijective or results in an error.

Historical Background⌗

Reversible computing has long been a topic that has been worked on to some degree for a couple of reasons. Early [Bennet] argued that a computer only had to dissipate heat when erasing information, since you have to keep all information to keep a given computation reversible this was given as an example of a future, more efficient system. Even if it had to do more actual computations to compute the same information.

More recently reversible programming languages have shown up in the field of quantum computers, again because of the need to keep all information at any given point in a computation. Though they are often a lot lower level than the languages I will present here, in theory these languages would be able to run on a powerful enough quantum computer.

Reversible Programming Languages⌗

The reversible languages we will look at in this post are not the ones used for quantum computers, we will look at some that are higher level.

Janus⌗

The first one I have here is Janus, it is made for general invertibility and I will go further into how it works in a later section.

Reversible Erlang⌗

Reversible Erlang is a subset of Erlang that introduces the concept of rollbacks. By using that the subset is reversible it is possible to rollback to a checkpoint by running in reverse until you hit it. Lanese2018.

Hermes⌗

Hermes is a small reversible programming language constructed to be used to implement encryption algorithms. It uses the reversibility and type system to defend against certain types of side-channel attacks. MOGENSEN2022102746

Janus⌗

Janus is a reversible programming language first described at Caltech around 1982 and formalized in 2007. [Lutz86, Yokoyama2007]

The main reversible language I will focus on is Janus, this is because I am using the general idea of that to implement the reversibility in my language.

Example⌗

We start with a small example of Janus, just to give a bit of taste of the syntax:

procedure copy(int arr[], int payload[])
    local int i = 0          // Create a local variable
    from i = 0 loop          // Loop from i == 0
        arr[i] += payload[i] // Add the value
        i += 1               // Increment counter
    until i = 2048           // until i == 2048
    delocal i = 2048         // Uninitialize local variable

How does Janus ensure reversibility?⌗

Janus uses specialized structures to ensure reversibility the first we will look at the constructs it uses for control flow. Janus has two types of control-flow: Conditionals and for-until loops. Furthermore, it uses the syntax to ensure reversibility, so we will look at that as well.

Conditionals⌗

To try to understand how conditionals work we will look at a small example and try to explain it. So we want to look at the following example:

if c₁ then
   s₁
else
   s₂
fi c₂

So what does this mean, we can look at it as c₁ as a pre-condition and c₂ as a post-condition. So if c₁ is true then s₁ is run and then c₂ must be true, and conversely, if c₁ is false then s₂ is run and c₂ must be false afterward. Another way we can look at it is by looking at a flow-chart:

In the flow-chart representation, we can see what we described above. Here we can also see how the inverse is going to look, we can swap c₁ with c₂, and then get the inverse of s₁ and s₂.

Loops⌗

The loops work similarly to the conditionals, though the conditions are slightly different compared to them. We again look at an example:

from c₁
  do s₁
  loop s₂
until c₂

This construct will probably seem a bit more alien to programmers, it is not clear what do and loop does in this context. To reverse the loop we swap c₁ and c₂ then we take the inverse of s₁ and s₂:

from c₂
  do I[s₁]
  loop I[s₂]
until c₁

Now we have an overview of how both directions will look, so we can try and follow the flow of it. For the forward we start with c₁ being true, and then it must be false every time following that until c₂ is true and the loop is terminated. The reason for this is that when we reverse the loop it will terminate too early if c₁ is ever true before what is the end of it when going forward.

We can also try and understand it by looking at a flow-chart as before:

The reason for the last part here is to ensure reversibility. To create the inverse version of this loop we swap c₁ and c₂, then take the inverse of s₁ and s₂.

Then we can see that we start with c₂ being true only once similarly to when it was the exit condition. And c₁ is true only when the loop is finished.

Syntax⌗

The Janus syntax is pretty barebones and not too complicated, so we will go over it here. It should be noted that the Janus version that we target has a few more features notable function arguments and locals, but we will come to them when we present RRust.

# Syntax Domains:
p ∈ Progs[Janus]
x ∈ Vars[Janus]
c ∈ Cons[Janus]
id ∈ Idens[Janus]
s ∈ Stmts[Janus]
e ∈ Exps[Janus]
⨁ ∈ ModOps[Janus]
⨀ ∈ Ops[Janus]

# Grammar
p ::= d* (procedure id s)⁺
d ::= x | x[c]
s ::= x ⨁= e | x[e] ⨁= e |
      if e then s else s fi e |
      from e do s loop s until e |
      call id | uncall id | skip | s s
e ::= c | x | x[e] | e ⨀ e
c ::= 0 | 1 | ... | 4294967295
⨁ ::= + | - | ^
⨀ ::= ⨁ | * | / | % | */ | & | '|' | && | "||" |
      < | > | = | != | <= | >=

The most interesting part of the syntax for me is the statements s, the first two forms it can take both cause mutation of a variable or an array. We can see that the only methods that are allowed to cause mutations are ⊕=, which again expands into +=, -= and ^=. These are the only operators that are allowed because they are the only ones that can be generally reversed. For expressions, all operators are allowed this is because they are not inversed when reversing the procedure. In s we also have call and uncall which allows us to both call a function and call the reverse of that function. Another interesting thing to note here is that we only allow the use of integers, this is because floating point numbers do not have reversible semantics.

Rust⌗

I will not dive too deep into Rust or its syntax in this section as there already exists good walkthroughs of the language which cover it well. Though I will get into the main parts of the language that enables its safety and explain them briefly. If you are an intermediate user of Rust you can probably skip or skim this section.

What Is Rust?⌗

The official site explains rust with this short motto:

A language empowering everyone to build reliable and efficient software.

Although this does not say too much about the language. Rust is a programming language first designed by Graydon Hoare and later incubated at Mozilla Research to be used in their products. The main feature of the language is to be safer than other languages in the same class such as C and C++. Today it is used widely in loads of companies such as Amazon and Discord.

Why Rust?⌗

So why should a company use Rust instead of the tested and stable languages like C and C++? One of the major reasons to use Rust is that it can rule out a class of issues related to memory safety, which is the cause of a lot of exploits. Microsoft for example has said that around 70% of their vulnerabilities are some form of memory corruption msrc_proactive_2019. Another reason to move to Rust is that it is a more “modern” language compared to C and C++ it has a bunch of features from functional languages such as pattern matching. It also has a more strict type system which again allows one to catch issues earlier. Furthermore, it has an integrated package manager and build system that makes it easier to pull in dependencies.

How does Rust ensure memory-safety?⌗

Rust uses a few different constructs to ensure safety here we will go through the most prominent.

Ownership⌗

Ownership is a concept that is central in Rust, it can be seen as a variable that every value has, and it follows a few rules:

• Each value in Rust has a variable that’s called its /owner/.
• There can be only one owner at a time.
• When the owner goes out of scope, the value will be dropped. So what do these rules tell us? Firstly every value has some /owner/ which must be unique for every value, and when it leaves a scope it is dropped. Dropped here means that a possible deconstructor is run, and it is deallocated.

Let us have a look at a small example of ownership.

let v = vec![1, 2, 3];
{              // start a new scope
    let w = v; // move v into the scope
}              // w goes out of scope and is dropped

v[0]           // Error

So in this example, we create a new value v which here is a Vec, it is a non-copy¹ type, so ownership is transferred into the new scope. There it is assigned to w which means that w now is the owner of the value. It is then dropped after it goes out of scope. Attempting to compile this code will end out with a compiler error:

error[E0382]: borrow of moved value: `v`
 --> src/main.rs:7:1
  |
2 |     let v = vec![1, 2, 3];
  |         - move occurs because `v` has type `Vec<i32>`, which does not implement the `Copy` trait
3 | { // start a new scope
4 |     let w = v; // move v into the scope
  |             - value moved here
...
7 | v[0] // Error
  | ^ value borrowed here after move

It is important that the error here happens at compile time as otherwise, this could cause a use-after-free memory corruption.

Borrowing⌗

To use the value of a non-copy type in a new scope without moving it you can use borrowing:

let v = vec![1, 2, 3];
{               // start a new scope
    let w = &v; // borrow v in the scope
}               // drop the reference to v

v[0] // No error

Here instead of moving the whole value into the new scope you only move a reference. A reference is similar to a pointer from other languages though it gives better guarantees at compile-time.

There are two types of borrows in Rust:

• &T Immutable references
• &mut T Mutable references There are a few rules related to those, immutable references may exist in any number as long as there are no mutable references. Mutable reference must be the only borrow of a value, no other borrows may exist at the same time.

To ensure that these rules are upheld Rust uses a system called the Borrow Checker. It will construct a set of regions called lifetimes in which a borrow is valid, it can then check if the rules are upheld there.

For example, if we try to use both a mutable and an immutable borrow at the same time we will run into an error:

let mut v0 = Vec::new();
v0.push(1);
let b0 = &v0[0];
let b1 = &mut v0[0];
println!("{}, {}", b0, b1);

Here both b0 and b1 are used at the same time leading to the following error:

error[E0502]: cannot borrow `v0` as mutable because it is also borrowed as immutable
 --> src/lib.rs:4:15
  |
3 | let b0 = &v0[0];
  |           -- immutable borrow occurs here
4 | let b1 = &mut v0[0];
  |               ^^ mutable borrow occurs here
5 | println!("{}, {}", b0, b1);
  |                    -- immutable borrow later used here

If either of b0 or b1 is removed from line 5 it will result in a successful compilation since the borrow checker can see that none of the borrowing rules are breached.

Unsafe⌗

In any case, where there is a possibility of breaking memory safety it is necessary to use the unsafe keyword which allows one to use functions and methods that are marked in that way. For example, it is unsafe to read from a raw pointer.

Bound checking⌗

The last thing I will highlight that Rust does to ensure safety is that array indexing is bound checked and will cause a run-time panic if it fails, thus aborting the program².

Meta-Programming⌗

The last feature of Rust I will highlight here does not have much to do with safety, it instead concerns the powerful meta-programming Rust allows. Rust has two major types of meta-programming:

macro_rules!⌗

• Can match on tokens and types of tokens.
• Can produce code following that.
• Is built into the compiler.
• Needs to be hygenic

Procedural Macros⌗

• Can do arbitrary transformations of a stream of tokens.
• Works as a compiler plugin.
• Often uses a library like syn to parse the tokens into a token tree.
• Can be unhygienic

RRust⌗

So now we have looked at reversible computing and the language Janus. We also had a detour into Rust and a few features for how it ensures safety. Now I will give some reasoning as to why I made RRust and how it solves issues with Janus, then I will finally present RRust.

Issues With The Safety Of Janus⌗

Janus has two modes of evaluation a safe interpreter that runs the code and a translation into C++. The translation into C++ gives us some issues when it comes to memory safety. If we for example have a function with the following signature:

procedure copy(int arr[], int payload[])

The C++ will generate the following functions:

void copy_forward(int *arr, int *payload);
void copy_reverse(int *arr, int *payload);

Here we see a few issues, C and C++ allow for mutable aliasing, so there is nothing to stop arr and payload from referencing the same memory, either in full or partially. In both cases, it could cause operations that damage the reversibility of the program. The other main issue is that it allows out-of-bound writing since it uses direct array access.

The Idea⌗

The idea I have is to use the safety features of Rust to ensure that it is memory-safe. Rust checks for out-of-bound access and mutable aliasing is not possible³.

To implement the language I will use the meta-programming features of Rust to transform the code into a reversible version.

How could a translation look?⌗

We will start by looking at the example from before:

procedure copy(int arr[], int payload[])
    local int i = 0
    from i = 0 loop
        arr[i] += payload[i]
        i += 1
    until i = 2048
    delocal int i = 2048

This function copies by addition from payload into arr. With the Rust version, we want to make it similar to how Janus translates it. We use a zero-sized type as a kind of namespace for the functions instead of using a prefix:

struct Copy; // Zero Sized Type
impl Copy {
    fn forward(arr: &mut [i32], payload: &mut [i32]) { /* forward code */ }
    fn backwards(arr: &mut [i32], payload: &mut [i32]) { /* backwards code */ }
}

To have it only mutate through a mutable reference instead of taking ownership and returning a value simplifies the code. This also means that it is not possible to alias arr with payload since it would in that case not compile.

I will also show how the forward and backwards code could look, it is very similar to how the same program would look in C++, The biggest difference is that arrays are bound checked⁴:

struct Copy;
impl Copy {
    fn forward(arr: &mut [i32], payload: &mut [i32]) {
        let mut i = 0;
        assert!(i == 0);
        while !(i == 2048) {
            arr[i] += payload[i];
            i += 1;
            assert!(!(i == 0));
        }
        if i != 2048 {
            panic!("Delocal failed {} != {}", i, 2048);
        }
        drop(i);
    }
    fn backwards(arr: &mut [i32], payload: &mut [i32]) {
        let mut i = 2048;
        assert!(i == 2048);
        while !(i == 0) {
            i -= 1;
            arr[i] -= payload[i];
            assert!(!(i == 2048));
        }
        if i != 0 {
            panic!("Delocal failed {} != {}", i, 0);
        }
        drop(i);
    }
}

How would this program look in RRust?⌗

Now we have a good idea about how the finished program should look, but the bigger question now is how it should look before being transformed into that. We can base the structure upon Janus with a flavor of Rust, so here I present the example from above in RRust:

rfn!(Copy, (arr: &mut [i32], payload: &mut [i32]), {
    let mut i = 0;
    rloop!(i == 0,
           {
               arr[i] += payload[i];
               i += 1;
           },
           i == 2048);
    delocal!(i, 2048);
});

We use a series of macros to construct each part of it, rfn! creates the structure of the code, rloop! creates a reversible loop with a pre-condition and a post-condition and delocal! creates checks if the value is correct and makes it impossible to use the local value afterward.

To ensure that the program was reversible I made a secondary transpiler that compiled the Rust code into Janus which could then also be checked.

Defining a syntax⌗

I created a syntax of the part of Rust I deemed to be compatible with Janus since I was translating to that as well:

program ::= rfn!( name, (args), body);
args ::= arg | args, arg
arg ::= id: &mut type
list ::= [ scalar ]
scalar ::= i8 | i16 | i32 | i64 | u8 | u16 | u32 | u64 | isize | usize
number ::= scalar :: MIN | scalar :: MIN + 1 | ... | 
           scalar :: MAX -1 | scalar :: MAX
name ::= [A-Z|a-z][A-Z|a-z|0-9|_]*
body ::= { stmt }
stmt ::= stmt ; | stmt ; stmt | { stmt } | * stmt | let id = expr |
         id ⊕= expr | l[expr] ⊕= expr |
         rif | rloop | delocal | name::forward(fargs) |
         name::backwards(fargs) | swap(id, id)
expr ::= number | *expr | l[expr] | expr ⊙ expr
fargs ::= farg | fargs, farg
farg ::= expr | id
⊕ ::= + | - | ^
⊙ ::= ⊕ | * | / | & | '|'
⊗ ::= == | >= | <= | < | > | !=
rif ::= rif!(bool, body, bool) | rif!(bool, body, body, bool)
rloop ::= rloop!(bool,body,bool) | rloop!(bool,body,body,bool)
delocal ::= delocal!(id, expr)
bool ::= expr ⊗ expr | true | false

Here the most important parts to observe are the two statements that allow mutation both uses the ⊕= that we saw with Janus as well. As well as only allowing integer types for the same reason as Janus.

Transformation⌗

So to facilitate the transformation of the code we use a few different features of the way that the language is set up. Local Inversibility, local invertibility here means that any syntax segment can be inversed in isolation, and there is no need for full program analysis to figure out how to translate a part, this also makes the second feature fit right in. I use recursive decent to go through the program and transform it. So in each part we do the local inversion, and then we recursively invert every part of that statement.

These two parts make it possible to transform the code. The only thing missing now is the rules we apply to perform these transformations. I want to define two sets of transformations one to Rust that follows the semantics of the translation into C++ and one that translates into Janus.

RRust to Rust⌗

In this section, I will present the transformation rules that go from RRust into Rust. I will be using F[stmt] for forward translation rules and R[stmt] for reverse translation.

Reversible If⌗

The first construct we will look at is reversible if statements, as with Janus, they have a pre and a post condition, here the pre-condition is c₁ and the post-condition is c₂.

rif!(c₁, b₁, b₂, c₂);

This then gets expanded into the following Rust code:

if c₁ {
  F[b₁]
  assert!(c₂);
} else {
  F[b₂]
  assert!(!(c₂));
}

We can see here that it is as with the graph we looked at earlier, if c₁ then c₂ and if !c₁ then !c₂.

This was the forward translation, the reverse translation is similar, but we exchange c₁ and c₂ and recursivly reverse:

if c₂ {
  R[b₁]
  assert!(c₁);
} else {
  R[b₂]
  assert!(!(c₁));
}

Here we can see that the same rules applies as well, e.g. if c₂ then c₁.

Reversible loop⌗

The reversible loop again works as the one in Janus, it has a condition that is only true when entering and a post-condition that similarily is only when exiting the loop.

rloop!(c₁, b₁, b₂, c₂);

This expands in the forward direction to:

assert!(c₁);
F[b₁];
while !(c₂) {
  F[b₂];
  assert!(!(c₁));
  F[b₁];
}

Here we have the form of loop we saw on the graph earlier, c₁ must be true entering and c₂ must be true when exiting. Again the reverse version is very similar. We only swap c₁ and c₂ around and recursively reverse.

assert!(c₂);
R[b₁];
while !(c₁) {
  R[b₂];
  assert!(!(c₂));
  R[b₁];
}

Other constructs⌗

Now we have looked at the biggest constructs, now we look at all the smaller ones and try to put a few words to each of why they are constructed in that way. We only need to go through the reverse translation as the forward translation has no changes. I will start with arguable one of the most important ones:

• R[s₁; s₂] We need to split them apart and then swap the positions since we need to do all operations in the reverse order: R[s₂]; R[s₁].
• R[s₁;] The semicolon is moved out and then recursively translated: R[s₁];.
• R[{ s₁ }] Here we also move the brackets out: { R[s₁] }.
• R[* s₁] We also do that with dereferences: * R[s₁].
• R[let id₁ = e₁] let statements will be switched to be after the delocal statement, so we need to swap them around: delocal!(id₁, e₁).
• R[delocal!(id₁, e₁)] and the reverse is the same: let id₁ = e₁.
• R[id₁ ⊕= e₁] Mutating statements gets the operators transformed: id R[⊕] e₁.
• R[l[e₁] ⊕= e₂] And similarly with list mutation: l[e₁] R[⊕]= e₂.
• R[name::forward(f₁)] Forward calls gets transformed into reverse calls: name::backwards(f₁).
• R[name::backwards(f₁)] and reverse calls gets transformed into forward calls: name::forward(f₁).
• R[swap(id₁, id₂)] Swap is its own self-inverse so no changes with it: swap(id₁, id₂).

Operators⌗

The 3 operators we skipped over are not translated in any complicated way, + becomes -, and the reverse is the same. For xor ^ it is similar to swap since it is self-inverse, so it does not change.

Aliasing⌗

The transformations done in the previous sections is enough to write reversible programs, but it does not remove the possibility to write programs that will not be reversible. To ensure this we need to insert checks for aliasing as we discussed in the Janus section. The Janus-generated C++ code will not check for it at any point, so it is possible to give inputs that will cause issues. Rust ensures that we cannot give aliased arguments, but we also need mutation operations not to be aliased. The specific forms that we need to ensure are the following:

// Also the case for +, - and ^.

a += b; // where a == b

l[x] += l[y]; // where x == y

To ensure this we insert a check if they point to the same value:

if core::ptr::eq(&(e₁), &(e₂)) {
    panic!();
}
e₁ += e₂;

Here the references will be implicit cast to pointers which we then can check for equality, and fail if they are equal.

RRust to Janus⌗

As said further up, I also implemented a transformation of RRust into Janus. The transformation was rather mechanical and was mostly done by removing all the extra notation Rust uses. The most complicated part of that was the parser needed for the macros. I am not going to fully present it here, but if you are interested in seeing more about it feel free to contact me about it.

Example RRust programs⌗

Here are a few examples of RRust code, they are reworked examples of Janus code.

rfn!(Fib, (x1: &mut i32, x2: &mut i32, n: &mut i32), {
    rif!(
        *n == 0,
        {
            *x1 += 1;
            *x2 += 1;
        },
        {
            *n -= 1;
            Fib::forward(x1, x2, n);
            *x1 += *x2;
            std::mem::swap(x1, x2);
        },
        *x1 == *x2
    );
});

let mut x1 = 0;
let mut x2 = 0;
let mut n = 10;

Fib::forward(&mut x1, &mut x2, &mut n);

assert_eq!(x1, 89);
assert_eq!(x2, 144);
assert_eq!(n, 0);

Fib::backwards(&mut x1, &mut x2, &mut n);

assert_eq!(x1, 0);
assert_eq!(x2, 0);
assert_eq!(n, 10);

rfn!(Factor, (num: &mut usize, fact: &mut [usize; 20]), {
    let mut tryf = 0;
    let mut i = 0;
    rloop!(
        tryf == 0 && *num > 1,
        {
            NextTry::forward(&mut tryf);
            rloop!(
                fact[i] != tryf,
                {
                    i += 1;
                    fact[i] += tryf;
                    let mut z = *num / tryf;
                    std::mem::swap(&mut z, num);
                    delocal!(z, *num * tryf);
                },
                *num % tryf != 0
            );
        },
        tryf * tryf > *num
    );

    rif!(
        *num != 1,
        {
            i += 1;
            fact[i] ^= *num;
            *num ^= fact[i];
            fact[i] ^= *num;
        },
        {
            *num -= 1;
        },
        fact[i] != fact[i - 1]
    );

    rif!(
        (fact[i - 1] * fact[i - 1]) < fact[i],
        {
            rloop!(
                tryf * tryf > fact[i],
                {
                    NextTry::backwards(&mut tryf);
                },
                tryf == 0
            );
        },
        {
            tryf -= fact[i - 1];
        },
        (fact[i - 1] * fact[i - 1]) < fact[i]
    );

    ZeroI::forward(&mut i, fact);
    delocal!(i, 0);
    delocal!(tryf, 0);
});

rfn!(ZeroI, (i: &mut usize, fact: &mut [usize; 20]), {
    rloop!(
        fact[*i + 1] == 0,
        {
            *i -= 1;
        },
        *i == 0
    );
});

rfn!(NextTry, (tryf: &mut usize), {
    *tryf += 2;
    rif!(
        *tryf == 4,
        {
            *tryf -= 1;
        },
        *tryf == 3
    );
});

let mut num = 840;
let mut fact = [0; 20];

Factor::forward(&mut num, &mut fact);
print!("Num: {}, Factors: ", num);
for i in 1u64..=6 {
    print!("{}: {}", i, fact[i as usize]);
    if i != 6 {
        print!(", ");
    } else {
        println!(".");
    }
}

// Num: 0, Factors: 1: 2, 2: 2, 3: 2, 4: 3, 5: 5, 6: 7.

Factor::backwards(&mut num, &mut fact);
print!("Num: {}, Factors: ", num);
for i in 1u64..=6 {
    print!("{}: {}", i, fact[i as usize]);
    if i != 6 {
        print!(", ");
    } else {
        println!(".");
    }
}

// Num: 840, Factors: 1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0.

Conclusion⌗

So what did I show with this whole blog? And did it reach the goals I had set for myself?

I have shown that it is possible to use the meta-programming of Rust to construct a safe reversible programming language, or at least one safer than the code generated by the language Janus. Following that I have shown that it is possible to use meta-programming in Rust for more advanced program transformations.

But some parts that I wanted to have shown are still missing, I believe it is possible to use the type system of Rust to ensure reversibility better than what I have done, specifically the need to ensure that a type is not Copy since that will break the rules. I have tried various things, but I never found a way that did not get in the way when writing code or was in some sense trivial to misuse.

Looking forward⌗

I have put the code up on GitHub at https://github.com/erk-/rrust, and I intend to work on it when I have some time. I have a few things that I want to have done with it including finding a way to make better bounds with the help of the type system. Any contributions are appreciated.

The main things that I want to do looking forward are, in no particular order:

• Use the type system of Rust to ensure types are not copied.
• Return errors instead of panicking when ending up in an error state.
  • A side effect of this will be the need to be able to mark input values as poisoned, since the value cannot be used after it enters a fail
• Allow functions and methods that do not mutate, for example there is no reason that it should be impossible to call len on a slice since it will be the same forward and in reverse. I believe that this is correct for any function that does not mutate, barring internal mutability.

Citations:⌗

The thermodynamics of computation — a review⌗

[web]

Computers may be thought of as engines for transforming free energy into waste heat and mathematical work. Existing electronic computers dissipate energy vastly in excess of the mean thermal energykT, for purposes such as maintaining volatile storage devices in a bistable condition, synchronizing and standardizing signals, and maximizing switching speed. On the other hand, recent models due to Fredkin and Toffoli show that in principle a computer could compute at finite speed with zero energy dissipation and zero error. In these models, a simple assemblage of simple but idealized mechanical parts (e.g., hard spheres and flat plates) determines a ballistic trajectory isomorphic with the desired computation, a trajectory therefore not foreseen in detail by the builder of the computer. In a classical or semiclassical setting, ballistic models are unrealistic because they require the parts to be assembled with perfect precision and isolated from thermal noise, which would eventually randomize the trajectory and lead to errors. Possibly quantum effects could be exploited to prevent this undesired equipartition of the kinetic energy. Another family of models may be called Brownian computers, because they allow thermal noise to influence the trajectory so strongly that it becomes a random walk through the entire accessible (low-potential-energy) portion of the computer’s configuration space. In these computers, a simple assemblage of simple parts determines a low-energy labyrinth isomorphic to the desired computation, through which the system executes its random walk, with a slight drift velocity due to a weak driving force in the direction of forward computation. In return for their greater realism, Brownian models are more dissipative than ballistic ones: the drift velocity is proportional to the driving force, and hence the energy dissipated approaches zero only in the limit of zero speed. In this regard Brownian models resemble the traditional apparatus of thermodynamic thought experiments, where reversibility is also typically only attainable in the limit of zero speed. The enzymatic apparatus of DNA replication, transcription, and translation appear to be nature’s closest approach to a Brownian computer, dissipating 20–100kT per step. Both the ballistic and Brownian computers require a change in programming style: computations must be renderedlogically reversible, so that no machine state has more than one logical predecessor. In a ballistic computer, the merging of two trajectories clearly cannot be brought about by purely conservative forces; in a Brownian computer, any extensive amount of merging of computation paths would cause the Brownian computer to spend most of its time bogged down in extraneous predecessors of states on the intended path, unless an extra driving force ofkTln2 were applied (and dissipated) at each merge point. The mathematical means of rendering a computation logically reversible (e.g., creation and annihilation of a history file) will be discussed. The old Maxwell’s demon problem is discussed in the light of the relation between logical and thermodynamic reversibility: the essential irreversible step, which prevents the demon from breaking the second law, is not the making of a measurement (which in principle can be done reversibly) but rather the logically irreversible act of erasing the record of one measurement to make room for the next. Converse to the rule that logically irreversible operations on data require an entropy increase elsewhere in the computer is the fact that a tape full of zeros, or one containing some computable pseudorandom sequence such as pi, has fuel value and can be made to do useful thermodynamic work as it randomizes itself. A tape containing an algorithmically random sequence lacks this ability.

Microsoft Security Response Center. A proactive approach to more secure code.⌗

https://msrc-blog.microsoft.com/2019/07/16/a-proactive-approach-to-more-secure-code/

Ivan Lanese, Naoki Nishida, Adrián Palacios, and Germán Vidal. A theory of reversibility for erlang. CoRR, abs/1806.07100, 2018.⌗

arXiv

In a reversible language, any forward computation can be undone by a finite sequence of backward steps. Reversible computing has been studied in the context of different programming languages and formalisms, where it has been used for testing and verification, among others. In this paper, we consider a subset of Erlang, a functional and concurrent programming language based on the actor model. We present a formal semantics for reversible computation in this language and prove its main properties, including its causal consistency. We also build on top of it a rollback operator that can be used to undo the actions of a process up to a given checkpoint.

Christopher Lutz. Janus: a time-reversible language. 1986. Letter to R. Landauer.⌗

.pdf

JANUS is a compiler and interpreter for the time-reversible language JANUS. The JANUS compiler is written in SLIMEULA, and compiles the code into an internal SLIMEULA Class structure which can be interpreted directly. ‘SLIMEULA’ means SIMULA running on a DECSYSTEM-20. JANUS is considered to be a throw-away piece of code. It will not be maintained and is not purported to be robust. The compiler consists of four major parts: A lexical analyzer which tokenizes the input stream and generates a symbol table; a recursive descent parser made of the Init Code of SLIMEULA Classes; an interpreter which consists of the procedure ’exec’ com- mon to all of the Classes created in the parsing; and the runtime command scanner

Tetsuo Yokoyama and Robert Glück. A reversible programming language and its invertible self-interpreter. In Proceedings of the 2007 ACM SIGPLAN Symposium on Partial Evaluation and Semantics-Based Program Manipulation, PEPM ‘07, page 144–153, New York, NY, USA, 2007. Association for Computing Machinery.⌗

[DOI, web]

A reversible programming language supports deterministic forward and backward computation. We formalize the programming language Janus and prove its reversibility. We provide a program inverter for the language and implement a self-interpreter that achieves deterministic forward and backward interpretation of Janus programs without using a computation history. As the self-interpreter is implemented in a reversible language, it is invertible using local program inversion. Many physical phenomena are reversible and we demonstrate the power of Janus by implementing a reversible program for discrete simulation of the Schrödinger wave equation that can be inverted as well as run forward and backward.

Keywords: reversible computing, program inversion, non-standard interpreter hierarchy, self-interpreter, Janus, reversible programming language

Torben Ægidius Mogensen. Hermes: A reversible language for lightweight encryption. Science of Computer Programming, 215:102746, 2022.⌗

[DOI, web]

Hermes is a domain-specific language for writing lightweight encryption algorithms: It is reversible, so it is not necessary to write separate encryption and decryption procedures. Hermes uses a type system that avoids several types of side-channel attacks, by ensuring no secret values are left in memory and that operations on secret data spend time independent of the value of this data, thus preventing timing-based attacks. We show a complete formal specification of Hermes, argue absence of timing-based attacks (under reasonable assumptions), and compare implementations of well-known lightweight encryption algorithms in Hermes and C.

Keywords: Lightweight encryption, Side-channel attacks, Reversible programming languages, Domain-specific languages